MATEMATICAS

 Una función cuadrática es una función polinómica de segundo grado y tiene la siguiente forma:

$�(�)=�{�}^2+��+�$

siendo $�,$ $�$ y $�$ números reales y $�\mathrm{\ne }0.$

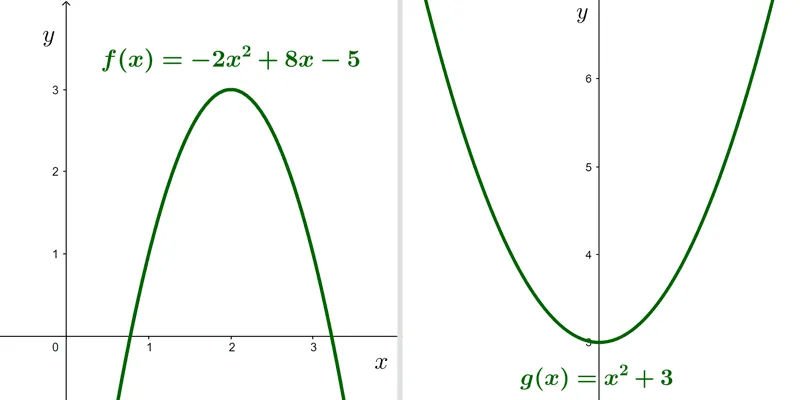
Algunos ejemplos de funciones cuadráticas son:

$�(�)=-2{�}^2+8�-5$

$�(�)={�}^2+3$

$ℎ(�)=6{�}^2$

$�=2�-{�}^2$

$�=-1+{�}^2+2�$

Una función como $�(�)=2�-9,$ no es cuadrática, puesto que no tiene término cuadrático. Tampoco lo es $�(�)={�}^3+3{�}^2-8�+5,$ porque, aunque tiene posee término cuadrático, no es un polinomio de segundo grado, sino de tercero.

Elementos y propiedades: Las funciones cuadráticas tienen una serie de elementos que determinan sus características y nos permiten estudiarla, estos elementos son:

• Coeficientes.
• Dominio y rango.
• Gráfica.
• Vértice.
• Eje de simetría.
• Raíces.
• Intersección con el eje y.

Coeficientes: Los coeficientes de una función cuadrática son los números reales a, b y c que aparecen en la fórmula general de la función, 

$�(�)=�{�}^2+��+�\mathrm{.}$ Cada uno de ellos tiene un nombre especial:

1. a es el coeficiente del término cuadrático o coeficiente principal. Nunca puede ser cero.
2. b es el coeficiente del término lineal. Puede ser cero.
3. c es el término independiente o constante. Puede ser cero.

Dominio y rango: El dominio de una función es el conjunto de todos los valores que puede tomar la variable independiente (generalmente denotada con x). El rango de una función es el conjunto de todos los valores que puede tomar la variable dependiente (generalmente denotada como y o f(x)).

El dominio de una función cuadrática es siempre el conjunto de los números reales, es decir, $\mathbb{�}\mathrm{.}$ El rango, en cambio, depende de los coeficientes, ya que estos determinarán los valores que tomará la función

Gráfica

La representación gráfica de una función cuadrática es una curva llamada parábola, la cual es simétrica respecto a una recta vertical que llamamos eje de simetría.

Cuando la parábola se abre "hacia arriba", se dice que la función es convexa. Si la parábola se abre "hacia abajo", la función es cóncava.

Dada una función cuadrática $�(�)=�{�}^2+��+�:$

La parábola abre hacia arriba si $�>0$
La parábola abre hacia abajo si $�<0$

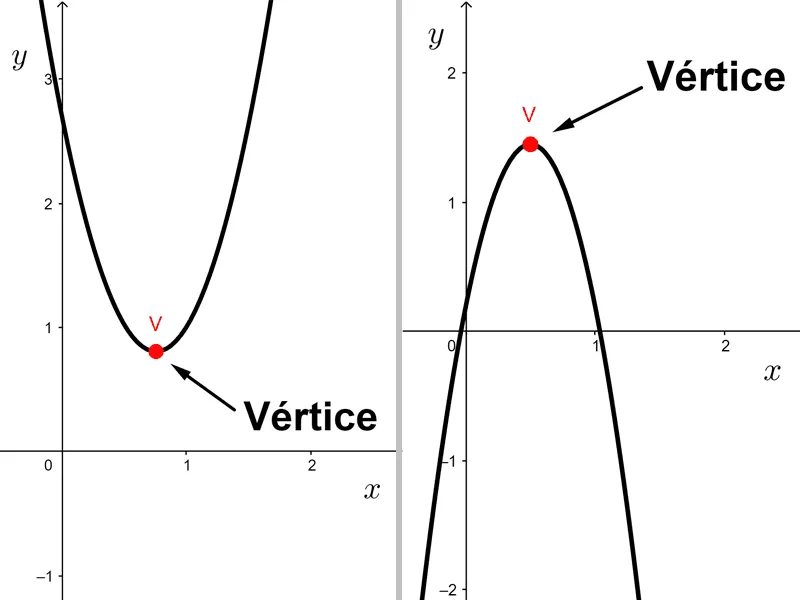
Vértice: El punto más bajo o más alto de la parábola se llama vértice. Este punto, por definición, es mínimo o máximo de la función, respectivamente.

El vértice V de la función $�(�)=�{�}^2+��+�$ tiene coordenadas $(ℎ,�)$ donde:

$ℎ={\displaystyle \frac{-�}{2�}}$

$�=�(ℎ)$

Si $�>0,$ el vértice es un mínimo de la función. Si $�<0,$ el vértice es un máximo.

Eje de simetría

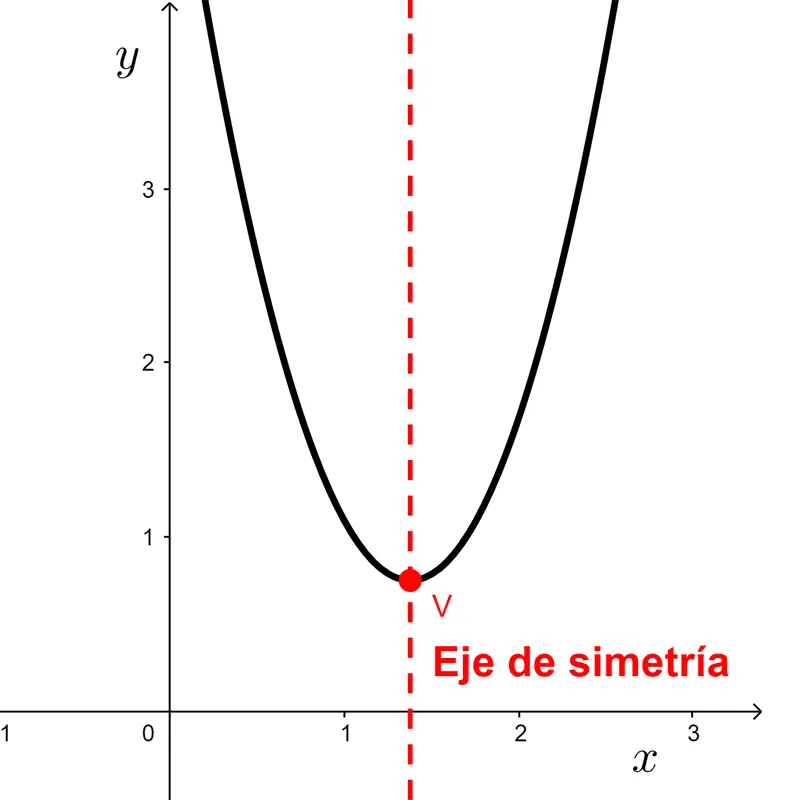
Decíamos anteriormente que la parábola es simétrica respecto a una recta vertical que llamamos eje de simetría (a veces se abrevia como "eje").

su ecuación es $�={\displaystyle \frac{-�}{2�}}$

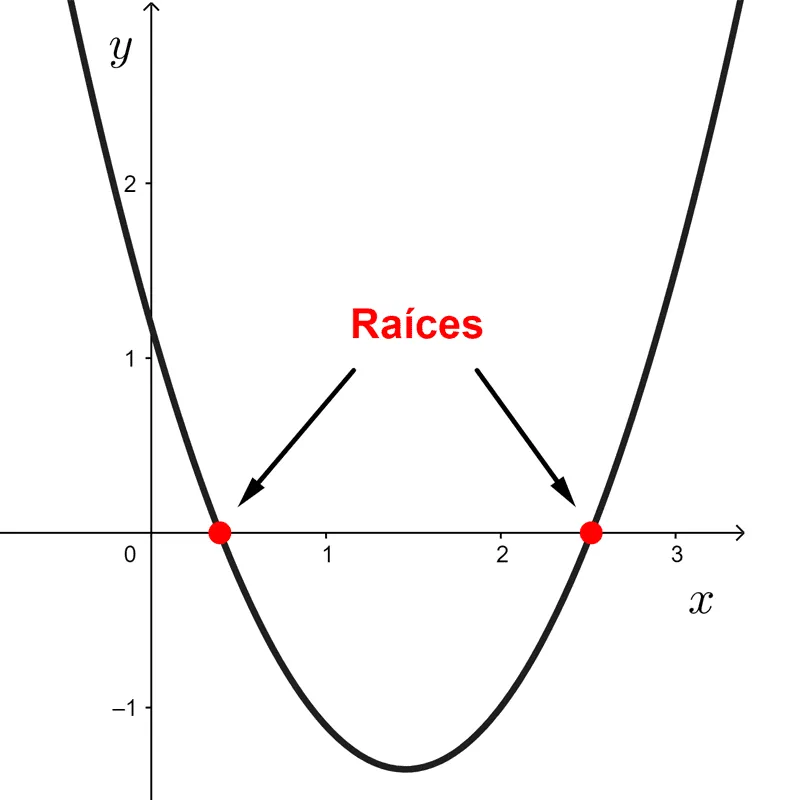
Raíces: Las raíces o ceros de una función son los valores de x donde ella se anula, es decir, 

$�(�)=0.$ En estos puntos la gráfica de la función corta al eje x.

Sustituyendo $�(�)$ por $0$ en una función cuadrática se obtiene la ecuación $�{�}^2+��+�=0.$ Esta puede ser resuelta mediante la fórmula resolvente para ecuaciones cuadráticas, también llamada fórmula general o de Bhaskara:

$�={\displaystyle \frac{-�\pm \sqrt{{�}^2-4��}}{2�}}$

$\mathrm{\Delta }={�}^2-4��$

Sea $�(�)=�{�}^2+��+�$ una función cuadrática y $\mathrm{\Delta }={�}^2-4��$ su discriminante:

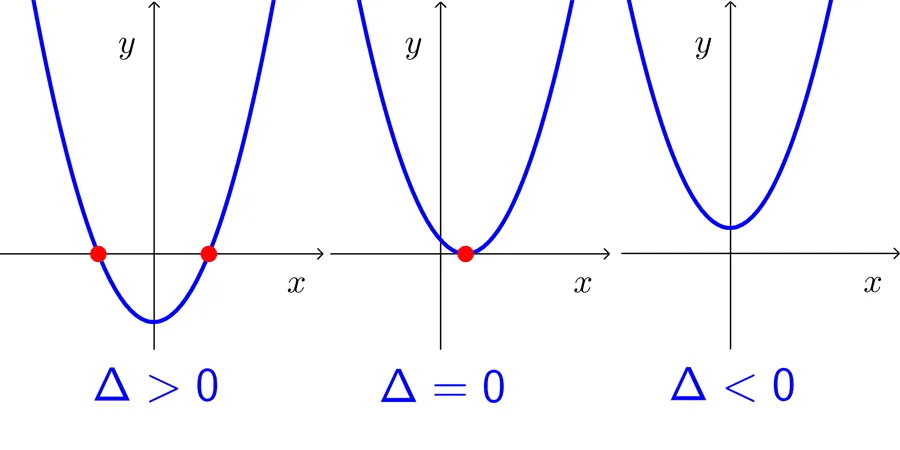
1. Si el discriminante es positivo, la función tiene dos raíces reales diferentes. Es decir, la gráfica cruza el eje x en dos puntos.
2. Si el discriminante es cero, la función tiene una raíz real de multiplicidad 2. Es decir, la gráfica toca al eje x en un punto.
3. Si el discriminante es negativo, la función no tiene raíces reales. Es decir, la gráfica no cruza ni toca al eje x.

Intersección con el eje y: La intersección de la gráfica de una función con el eje y, si existe, es única y se da cuando 

$�=0.$ Como el dominio de una función cuadrática es $\mathbb{�},$ el cero está en el dominio y su imagen es:

$�(0)=�(0{)}^2+�(0)+�=�$

Entonces, el corte de la gráfica de una función cuadrática con el eje y se da en el punto $(0,�)\mathrm{.}$ Algunas veces este punto es llamado ordenada al origen, aunque este nombre está reservado para las funciones lineales

ANTOLOGÍA

Como parte de los proyectos interdisciplinarios se realizo una recopilación de los temas vistos en este segundo parcial.

">